Introduction

You have probably seen one of these fish symbol stickers on some cars, or on the streets’ graffiti:

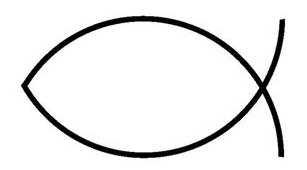
This is Icthus symbol in Christianity, also known as Vesica Piscis, and is a repeating pattern in Christian paintings of Jesus and saints. In this project we explore how this pattern formalized as a mathematical constant stretches beyond a particular religion and into the realm of universal, sacred geometry.

Finding where the fish came from...

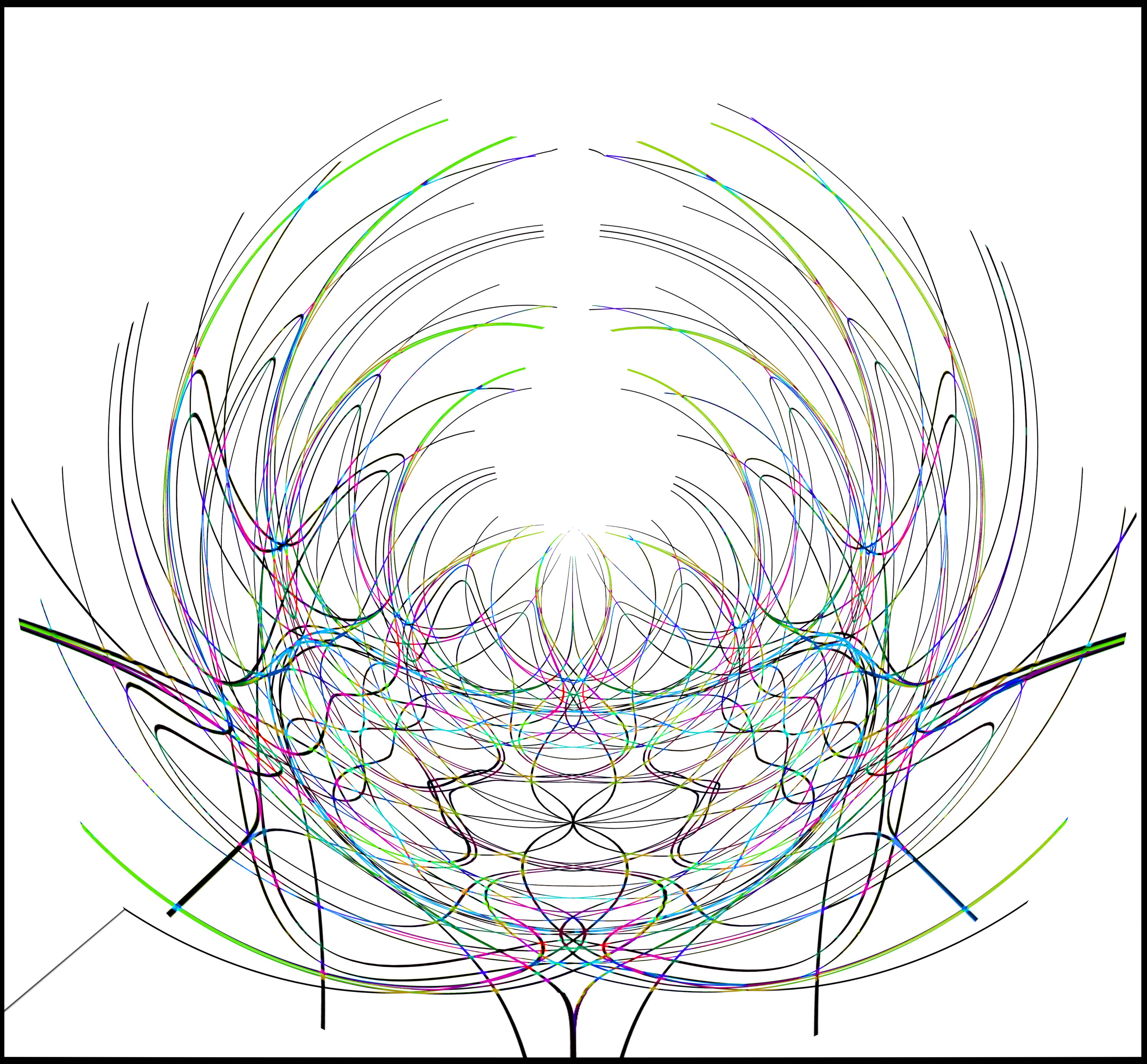
So, what’s this about?

We are a couple of quantum enthusiasts exploring a logical system where specific relationships between numerically related algebric equations generates an easily recognizable sphere theory.

Jason Chewning (Nymphoton) has explored these curves from the equations for the past 5 years, and explains the logical system in layman terms:

The square root of three is a constant that can be geometrically and trigonometrically identified, measured, represented. The Vesica Piscis is simply y = x / sqrt(3), and the logic system is an iteration of that constant. All the algebraic iterations in the logic system, when fully simplified, all comes down to y = x / sqrt(3). However when one starts off un-simplified version, one could alter the algebra and produce a number of distinctly related curves.

For instance, currently all the logic system is recorded in Geogebra in this way:

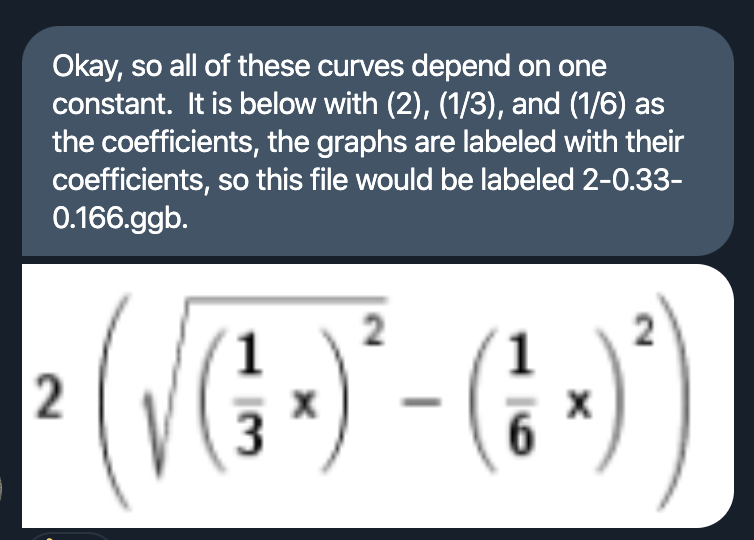
Taking above sample equation as U(x), then the entire spectrum of curves is:

• U(x) = 2sqrt((1/3x)^2) - (1/6x)^2 => positive function
• -U(x) => negative function
• 1/U(x) => reciprocal function
• -1/U(x) => negative reciprocal function
• +- x^U(x) => variable root function
• +- U(x)^x => variable exponent function
• +- Cos(x^(U(x))) ... all trigonmentric functions

Mapping it out yields the image below:

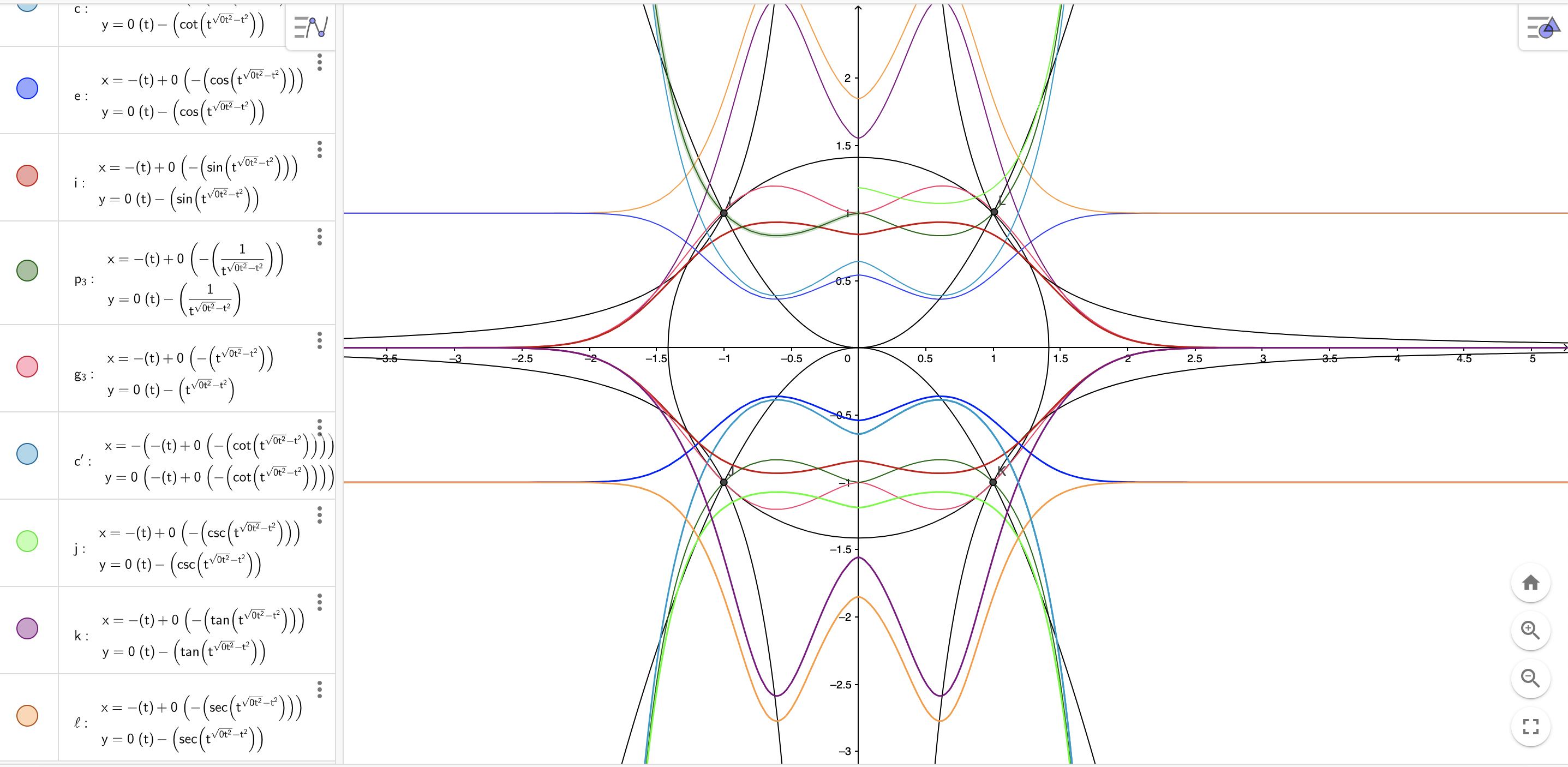
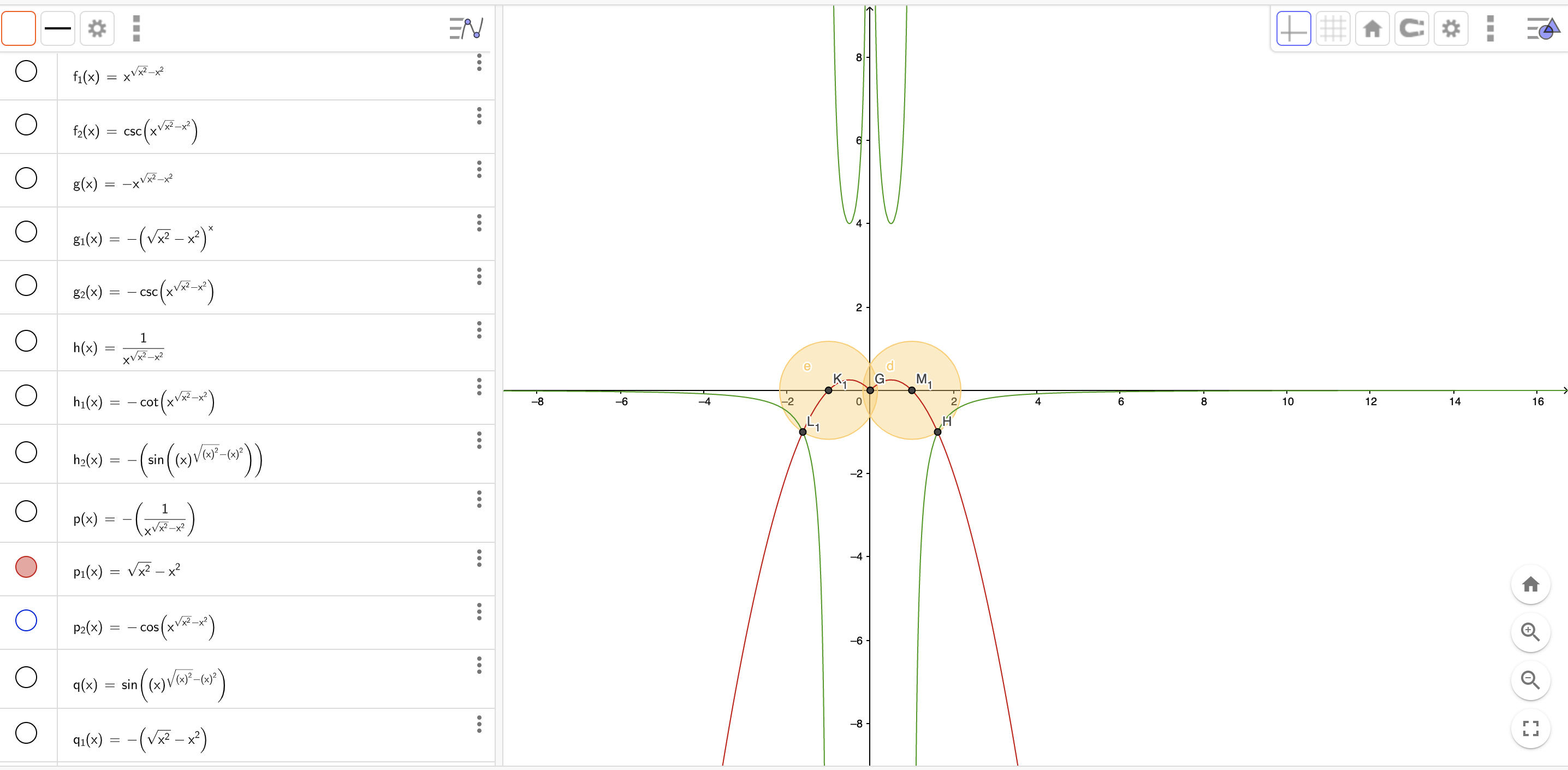
Stunning, but what does this mean? That’s what we’re trying to find out. Jason has first classified a bunch of iterations he did over the years into a “gate system” outlined below:

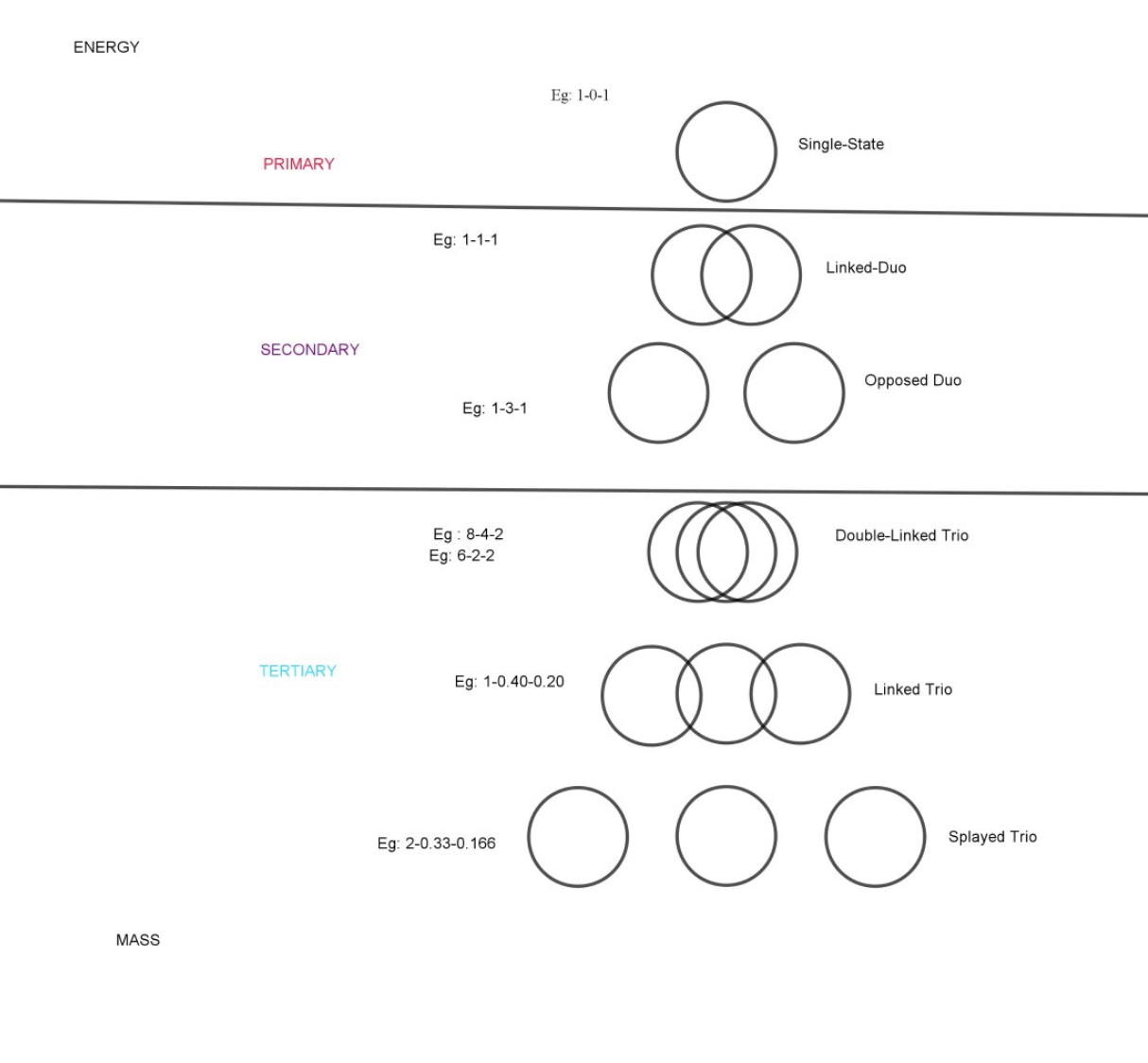
So the previous example was an example of ‘Splayed trio’, as you can see three distict circles not touching each other.

Single-state

Linked-Duo

Opposed-Duo

Next steps...

We will be

• adding a little interactive component using Idyll for a small sandbox-like environment to fiddle around on this website
• developing a backend engine to simulate more diverse iterations of these algebraic expressions;
• i.e plugging in coefficients, recording subsequent data and seeing where the graph fits into the gate system category, seeing how / where it changes in category as the parameters change.

If you’re interested in joining this project, please contact Jason (@Nymphoton) on Twitter!

Or if you have ideas / comments for the project, leave them on our public Notion board. You can also check our progress on the project there.